
This shows the most likely range of values that will occur if your data follows the null hypothesis of the statistical test. The t-value of the regression test is 2.36 – this is your test statistic.įor any combination of sample sizes and number of predictor variables, a statistical test will produce a predicted distribution for the test statistic. a t-value comparing that coefficient to the predicted range of regression coefficients under the null hypothesis of no relationship.ExampleTo test your hypothesis about temperature and flowering dates, you perform a regression test. However, formulas to calculate these statistics by hand can be found online. In practice, you will almost always calculate your test statistic using a statistical program (R, SPSS, Excel, etc.), which will also calculate the p-value of the test statistic. Null: The variation among two or more groups is greater than or equal to the variation between the groupsĪlternative: The variation among two or more groups is smaller than the variation between the groupsĪlternative: Two samples are not independent (i.e. Test statisticĪlternative: The means of two groups are not equalĪlternative:The means of two groups are not equal Types of test statisticsīelow is a summary of the most common test statistics, their hypotheses, and the types of statistical tests that use them.ĭifferent statistical tests will have slightly different ways of calculating these test statistics, but the underlying hypotheses and interpretations of the test statistic stay the same.
The t-value compares the observed correlation between these variables to the null hypothesis of zero correlation. To test this hypothesis you perform a regression test, which generates a t-value as its test statistic. Alternate hypothesis: There is a correlation between temperature and flowering date.Null hypothesis: There is no correlation between temperature and flowering date.You use a long-term data set that tracks temperature and flowering dates from the past 25 years by randomly sampling 100 trees every year in an experimental field. ExampleYou are testing the relationship between temperature and flowering date for a certain type of apple tree.
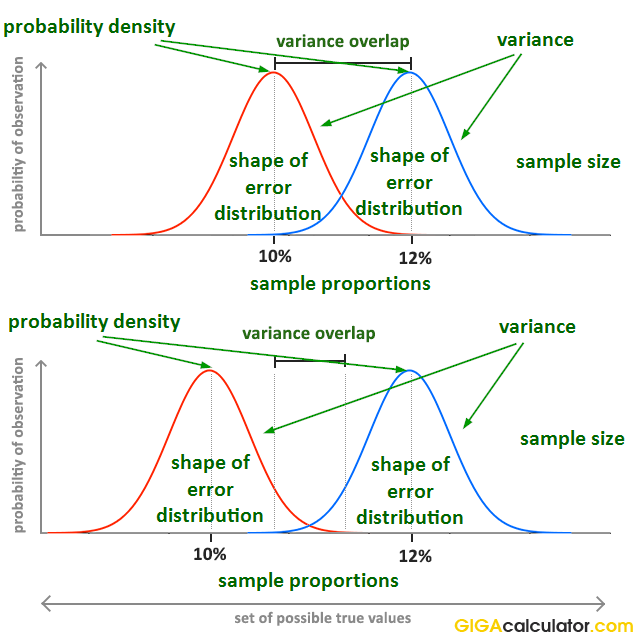
the correlation between variables or difference between groups) divided by the variance in the data (i.e. Generally, the test statistic is calculated as the pattern in your data (i.e. The test statistic summarizes your observed data into a single number using the central tendency, variation, sample size, and number of predictor variables in your statistical model. Different statistical tests predict different types of distributions, so it’s important to choose the right statistical test for your hypothesis. The distribution of data is how often each observation occurs, and can be described by its central tendency and variation around that central tendency.


 0 kommentar(er)
0 kommentar(er)
